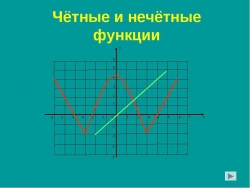
Презентация к уроку алгебры ,,Свойства функций. Четные и нечетные функции

Основные виды функций,
их графики и свойства.

Можно ли утверждать, что данный график задаёт функцию?
ОПРЕДЕЛЕНИЕ ФУНКЦИИ

Прочитайте график функции:
1. Область определения функции
D(y) = (- ; +)
2. Область значений функции
E(y) = (-4 ; +) E(y) = (- ; +)
3. Нули функции
у=0 при х = 0; ±1,4 у=0 при х = 0; ±1,2
4. Промежутки возрастания/
убывания функции
y при х [–1;0], [1;+] y при (– ;–1], [1;+]
y при x(–;-1], [0;1] y при х x[–1; 1]
5. Наибольшее/наименьшее
значение функции
унаим = –4; унаиб не сущ. Унаим , унаиб не сущ.
6. Ограниченность функции
Ограничена снизу Не ограничена
1 вариант
2 вариант
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ

А
Л
Ь
Т
С
П
А
Р
А
Б
О
Н
О
Б
Г
Р
А
Н
И
Ч
Е
Н
Н
О
С
Т
Ь
Н
Е
П
Р
Е
Р
Ы
В
Н
О
С
Е
О
Т
Ь
П
Р
Я
М
А
Я
И
Г
Л
А
О
Н
О
М
1. Название графика обратной пропорциональности.
1
2
3
4
5
6
2. Свойство функции, объединяющее возрастание и убывание.
3. Название графика линейной функции.
4. Свойство функции,
не имеющей разрывов.
5. Свойство функции, не имеющей значений выше или/и ниже данного.
6. Название графика квадратичной функции.
азминка

Укажите формулу, задающую
эту функцию:
ОСНОВНЫЕ ВИДЫ ФУНКЦИЙ И ИХ ГРАФИКИ

Укажите формулу, задающую
эту функцию:
ОСНОВНЫЕ ВИДЫ ФУНКЦИЙ И ИХ ГРАФИКИ

Укажите формулу, задающую
эту функцию:
Анимированные персонажи взяты с сайта: http://office.microsoft.com
ОСНОВНЫЕ ВИДЫ ФУНКЦИЙ И ИХ ГРАФИКИ

МОЛОДЦЫ!
Назовите уравнение функции, график которой изображён ниже:
ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

ЧЁТНОСТЬ
И
НЕЧЁТНОСТЬ
ФУНКЦИИ

Задачи урока:
- вывести определения чётной и нечётной функции;
- выяснить как эти свойства отражаются на графике функции;
- научиться доказывать свойства чётности аналитически.

Что же такое веб-квест?

«Quest» в переводе с английского языка — продолжительный целенаправленный поиск, который может быть связан с приключениями или игрой (это слово также служит для обозначения одной из разновидностей компьютерных игр).
С педагогической точки зрения, веб-квест — это проблемное задание, для выполнения которого используются информационные ресурсы Интернета.

Работа над квестом:
Цель: Надо систематизировать теоретические сведения о чётности и нечётности функций;
1. УЗНАТЬ:
определения понятий?
взаимосвязи изученных понятий с графиками функций?
зависимости, отражённые в формулировках утверждений, с формулами, задающими функцию?
2. СОЗДАТЬ:
компьютерную презентацию по теме;
опорный конспект темы
3. ОФОРМИТЬ ОТЧЁТ (доклад).

Задачи:

1.     организация работы в команде, распределение ролей;
2. поиск информации по конкретной теме; 
3.     разработка структуры презентации;
4.      создание материалов для презентации; 
5.     доработка материалов для презентации.
6. защита

Человек образованный – тот, кто знает, где найти то, чего он не знает.

Георг Зиммель

Итог урока.


- Какие функции называются четными?
- Какие функции называются нечетными?
- Как вы считаете, справились ли мы с задачами урока?
- Как оценивают работу каждого участника руководители групп?
- Как каждый из вас оценивает свое участие в коллективной работе?

Итог урока.
- Какие функции называются четными?
- Какие функции называются нечетными?
- Как вы считаете, справились ли мы с задачами урока?
- Как оценивают работу каждого участника руководители групп?
- Как каждый из вас оценивает свое участие в коллективной работе?



Итог урока.
- Какие функции называются четными?
- Какие функции называются нечетными?
- Как вы считаете, справились ли мы с задачами урока?
- Как оценивают работу каждого участника руководители групп?
- Как каждый из вас оценивает свое участие в коллективной работе?



Итог урока.
- Какие функции называются четными?
- Какие функции называются нечетными?
- Как вы считаете, справились ли мы с задачами урока?
- Как оценивают работу каждого участника руководители групп?
- Как каждый из вас оценивает свое участие в коллективной работе?

п 11,
работа с графиками – рис.51-55
№ 11

Прочитайте график функции:
1. Область определения функции
D(y) = (- ; +)
2. Область значений функции
E(y) = (-4 ; +) E(y) = (- ; +)
3. Чётность/нечетность функции
Чётная Нечётная
4. Нули функции
у=0 при х = 0; ±1,4 у=0 при х = 0; ±1,2
5. Промежутки возрастания/
убывания функции
y при х [–1;0], [1;+] y при (– ;–1], [1;+]
y при x(–;-1], [0;1] y при х x[–1; 1]
6. Наибольшее/наименьшее
значение функции
унаим = –4; унаиб не сущ. Унаим , унаиб не сущ.
7. Ограниченность функции
Ограничена снизу Не ограничена
8. Непрерывность функции
непрерывна
1 вариант
2 вариант
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ

f(-3) = f(3)
2) f(-2) < f(2)
3) f(0) > f(1)
4) f(x) >1 при -3 < x < 0

5) f(x)  1  0  x  3
Укажите номера верных утверждений:
ДРУГИЕ СВОЙСТВА ФУНКЦИИ

Линейная функция y = kx + b (k, b  R) График – прямая
Частные случаи:
y = kx (прямая пропорциональность)
График – прямая, походящая через начало координат
y = а (а  R) График – прямая, параллельная оси Ох
х = а (а  R) График – прямая, параллельная оси Оу

Обратная пропорциональность y = (k ≠ 0, x ≠ 0, y ≠ 0)
График – гипербола
Квадратичная функция y = ax2 + bx+ c (a, b, c  R; a≠0)
График – парабола
Степенная функция y = xn (n  N)
График – парабола или кубическая парабола
Степенная функция y = x– n (n  N)
Модуль y = |x|
Квадратный корень

Кубический корень

Основные виды функций и их графики:

Укажите формулу, задающую
эту функцию:
ОСНОВНЫЕ ВИДЫ ФУНКЦИЙ И ИХ ГРАФИКИ

Укажите формулу, задающую
эту функцию:
ОСНОВНЫЕ ВИДЫ ФУНКЦИЙ И ИХ ГРАФИКИ

МОЛОДЦЫ!
Назовите уравнение функции, график которой изображён ниже:
ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ