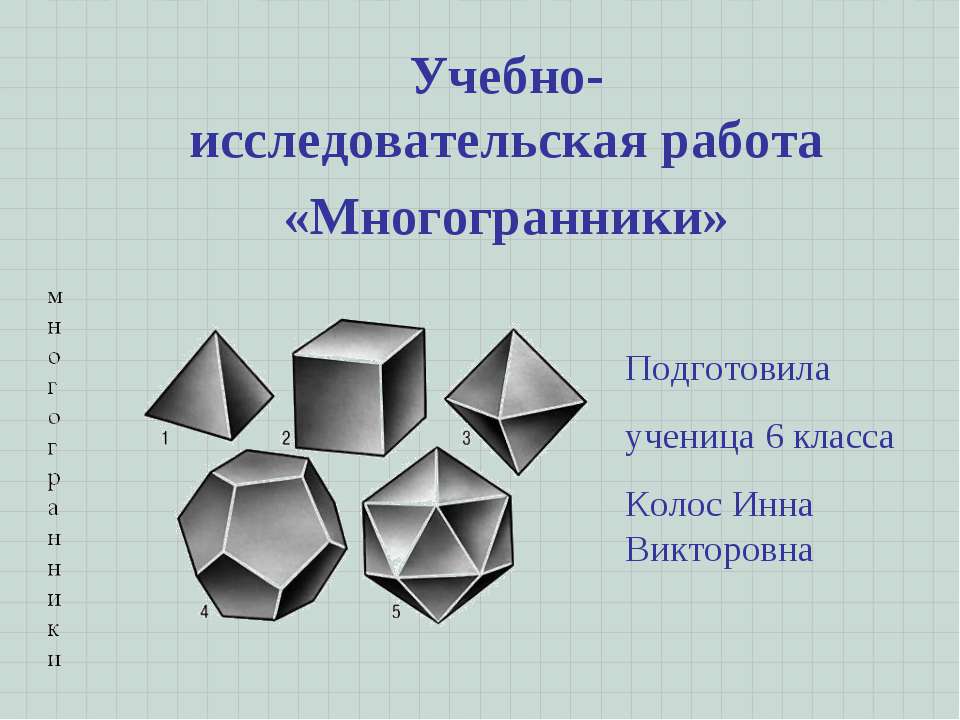
Учебно-исследовательская работа «Многогранники»

Учебно-исследовательская работа «Многогранники» Подготовила ученица 6 класса Колос Инна Викторовна

Введение При исследовании многогранников перед собой мы поставили следующие задачи: Изучить разновидности многогранников. Научиться строить некоторые модели многогранников. Исследовать вращающие кольца тетраэдров.

Многогранники С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.

Многогранник Это пространственное тело с плоскими гранями и прямолинейными ребрами, устроенное так, чтобы всякое ребро соединяет две вершины и служит общей стороной двух граней

Простейшими примерами многогранников служат пирамиды и призмы У пятиугольной призмы: 10 вершин 15 ребер 7 граней У пятиугольной пирамиды: 6 вершин 10 ребер 6 граней

Антипризма (призмоид) Основания одинаковые, но расположены различно: вершины каждого из оснований лежат над сторонами другого, так что боковые ребра идут зигзагом У пятиугольной антипризмы: 10 вершин 20 ребер 12 граней

Для любого выпуклого многогранника справедливо соотношение Г+В-Р=2 Г- число граней, В- число вершин, Р- число ребер данного многогранника Теорема Эйлера

Теорема Эйлера

Правильные многогранники Существует пять видов многогранников: {p,q} V (в) E (р) F (г) Название {3,3} 4 6 4 Правильный тетраэдр {4,3} 8 12 6 Куб {3,4} 6 12 8 Октаэдр {5,3} 20 30 12 Додекаэдр {3,5} 12 30 20 Икосаэдр

Правильные многогранники

Полуправильные многогранники (Архимедовы тела)

Другие тела Архимеда имеют более сложные названия:

Вращающие кольца тетраэдров Дж. М. Андреас и Р. М. Сталкер независимо друг от друга открыли семейство изгибаемых конечных многогранников с 2n вершинами, 6n ребрами и 4n треугольными гранями. Гранями служат грани n тетраэдров, соединенных между собой в циклическом порядке по определенным парам противоположных ребер каждого, так что получается фигура наподобие кольца.

Модель кольца из 6 тетраэдров При n=6 фигура ещё жесткая, поэтому полностью не выворачивается

Модель кольца из 8 тетраэдров

Заключение: Проводя исследования по данной теме, мы изучили исторические данные по многогранникам; При построении разверток многогранников мы научились работать с чертежными инструментами; Создавая модели призмы, антипризмы, пирамиды, а также вращающих колец из тетраэдров мы расширили свое пространственное воображение. В дальнейшей работе мы хотим научиться строить модели более сложных по виду многогранников.

Спасибо за внимание!