Следствия из аксиом
- Рубрика: Презентации / Презентации по Геометрии
- Просмотров: 223
Презентация для классов "Следствия из аксиом" онлайн бесплатно на сайте электронных школьных презентаций uchebniki.org.ua
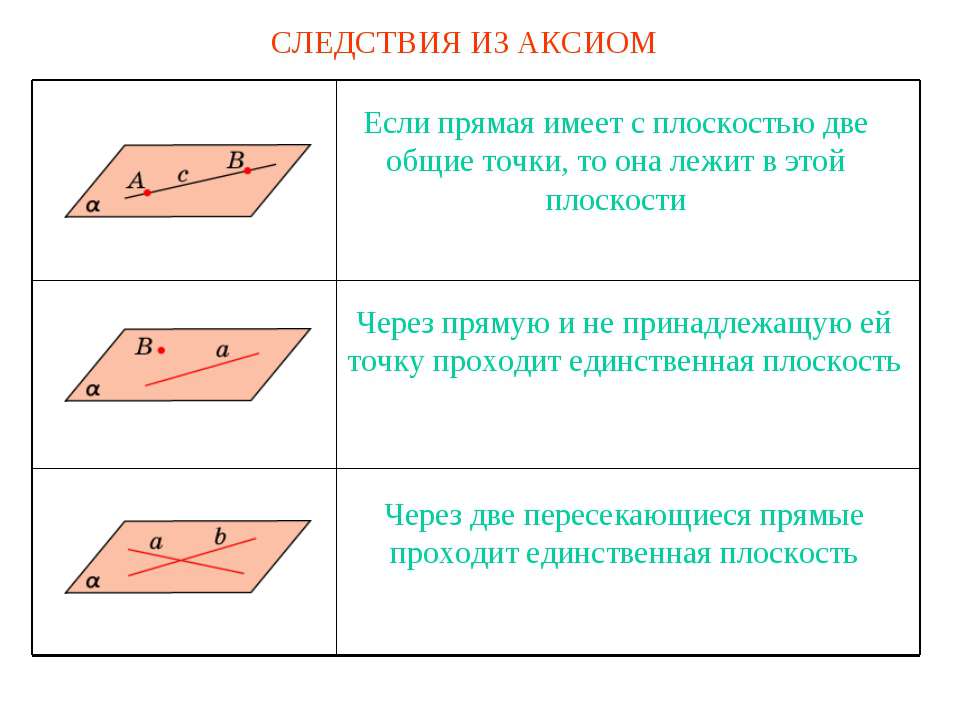
СЛЕДСТВИЯ ИЗ АКСИОМ Если прямая имеет с плоскостью две общие точки, то она лежит в этой плоскости Через прямую и не принадлежащую ей точку проходит единственная плоскость Через две пересекающиеся прямые проходит единственная плоскость
Упражнение 1 Четыре точки не принадлежат одной плоскости. Могут ли три из них принадлежать одной прямой? Ответ: Нет.
Упражнение 2 Три вершины параллелограмма принадлежат некоторой плоскости. Верно ли утверждение о том, что и четвёртая вершина этого параллелограмма принадлежит той же плоскости? Ответ: Да.
Упражнение 3 Две вершины и точка пересечения диагоналей параллелограмма принадлежат одной плоскости. Верно ли утверждение о том, что и две другие вершины параллелограмма принадлежат этой плоскости? Ответ: Да.
Упражнение 4 Могут ли вершины замкнутой ломаной, состоящей из трёх звеньев, не принадлежать одной плоскости? Ответ: Нет.
Упражнение 5 Могут ли вершины замкнутой ломаной, состоящей из четырёх звеньев, не принадлежать одной плоскости? Ответ: Да.
Упражнение 7 Прямые a, b, c попарно пересекаются. Верно ли, что они лежат в одной плоскости? Ответ: Нет.
Упражнение 8 Верно ли, что любая прямая, пересекающая каждую из двух данных пересекающихся прямых, лежит в плоскости этих прямых? Ответ: Нет.
Упражнение 9 Прямые a и b пересекаются в точке C. Через прямую a проходит плоскость , через прямую b – плоскость , отличная от . Как проходит линия пересечения этих плоскостей? Ответ: Через точку C.
Упражнение 12 Сколько плоскостей можно провести через четыре точки? Ответ: Или одну, или ни одной.
Упражнение 13 Сколько плоскостей можно провести через различные тройки из пяти точек, никакие четыре из которых не принадлежат одной плоскости? Ответ: 10.
Упражнение 14 На сколько частей делят пространство три плоскости, имеющие одну общую точку? Ответ: 8.




















