Центральное проектирование (перспектива)
- Рубрика: Презентации / Презентации по Геометрии
- Просмотров: 258
Презентация для классов "Центральное проектирование (перспектива)" онлайн бесплатно на сайте электронных школьных презентаций uchebniki.org.ua
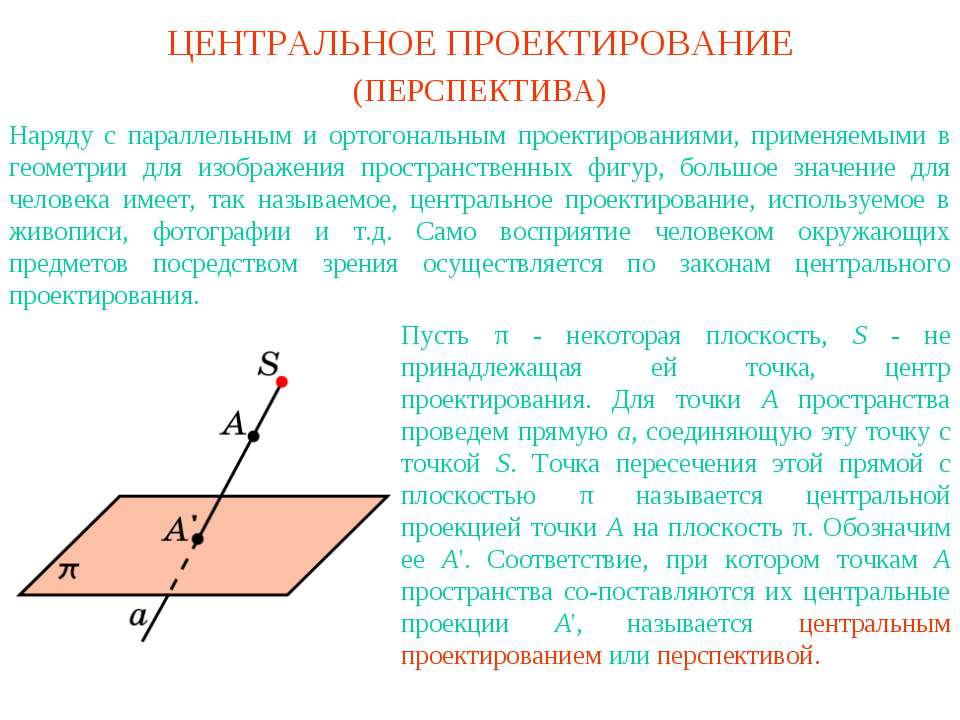
ЦЕНТРАЛЬНОЕ ПРОЕКТИРОВАНИЕ Наряду с параллельным и ортогональным проектированиями, применяемыми в геометрии для изображения пространственных фигур, большое значение для человека имеет, так называемое, центральное проектирование, используемое в живописи, фотографии и т.д. Само восприятие человеком окружающих предметов посредством зрения осуществляется по законам центрального проектирования. Пусть π - некоторая плоскость, S - не принадлежащая ей точка, центр проектирования. Для точки A пространства проведем прямую a, соединяющую эту точку с точкой S. Точка пересечения этой прямой с плоскостью π называется центральной проекцией точки A на плоскость π. Обозначим ее A'. Соответствие, при котором точкам A пространства со поставляются их центральные проекции A', называется центральным проектированием или перспективой. (ПЕРСПЕКТИВА)
Перспектива 1 Центральное проектирование плоской фигуры Ф на плоскость, находящуюся между плоскостью фигуры Ф и центром проектирования S.
Перспектива 2 Центральное проектирование плоской фигуры Ф в случае, когда центр проектирования S расположен между плоскостью фигуры Ф и плоскостью проектирования.
Перспектива 3 Центральное проектирование плоской фигуры Ф в случае, когда плоскость фигуры Ф расположена между плоскостью плоскостью проектирования и центром проектирования S.
А. Дюрер На гравюре А.Дюрера (1471 – 1528) показано получение перспективного изображения предмета с помощью натянутой нити.
Н.Н. Ге Русский художник и педагог Н.Н. Ге (1834 – 1894), обращаясь к своим ученикам, говорил: «Учите перспективу, и когда овладеете ею, внесите ее в работу, в рисование. Здесь мы представляем картину Н.Н. Ге «Петр I допрашивает царевича Алексея»
Упражнение 1 Для всех ли точек пространства существует центральная проекция? Для каких точек она не существует? Ответ: Нет. Она не существует для точек плоскости, проходящей через центр проектирования и параллельной плоскости проектирования.
Упражнение 2 Могут ли при центральном проектировании параллельные прямые перейти в пересекающиеся? Ответ: Да.
Упражнение 3 В каком случае центральной проекцией двух прямых будут две параллельные прямые? Ответ: Если прямые параллельны плоскости проектирования.
Упражнение 4 Какое изображение фигуры получится в центральной проекции, если плоскость проектирования расположена между фигурой и центром проектирования? Ответ: Уменьшенное прямое.
Упражнение 5 Какое изображение фигуры получится в центральной проекции, если центр проектирования находится между фигурой и плоскостью проектирования? Ответ: Перевернутое.
Упражнение 6 Какое изображение фигуры получится в центральной проекции, если она расположена между плоскостью проектирования и центром проектирования? Ответ: Увеличенное прямое.
Упражнение 7 Что можно сказать о центральной проекции плоской фигуры, которая расположена в плоскости, параллельной плоскости проектирования? Ответ: Она будет подобна исходной.
Упражнение 8 Пусть прямая a пересекает плоскость и не проходит через точку S. Покажите на рисунке, куда при центральном проектировании переходит часть прямой a, расположенная: а) «выше»; б) «ниже» плоскости . Ответ: а) В точки лучей AD’ и SC’ без их начал, т.е. без точек A и S; б) в точки отрезка AS без его концов, т.е. без точек A и S.
Упражнение 9 На рисунке изображена центральная проекция куба. Объясните, как в каждом случае расположен куб относительно плоскости проектирования. Ответ: а) Грань ADD1A1 куба параллельна плоскости проектирования; б) ребро BB1 куба параллельно плоскости проектирования; в) грань ABCD куба параллельна плоскости проектирования и точка F лежит внутри изображения этой грани; г) плоскость проектирования не параллельна никакому ребру куба.
Упражнение 10 На рисунке изображена центральная проекция правильной четырёхугольной пирамиды. Объясните, как она расположена относительно плоскости проектирования. Ответ: а) Плоскость основания пирамиды параллельна плоскости проектирования, и прямая SM перпендикулярна плоскости проектирования, где S – центр проектирования, M – вершина пирамиды; б) плоскость основания пирамиды параллельна плоскости проектирования; в) плоскость основания не параллельна плоскости проектирования.
Упражнение 11 На рисунке изображён прямой круговой цилиндр в центральной проекции. Объясните, как он расположен в каждом случае относительно плоскости проектирования. Ответ: а) Плоскость проектирования параллельна основаниям цилиндра; б) плоскость проектирования не параллельна основаниям цилиндра.


























