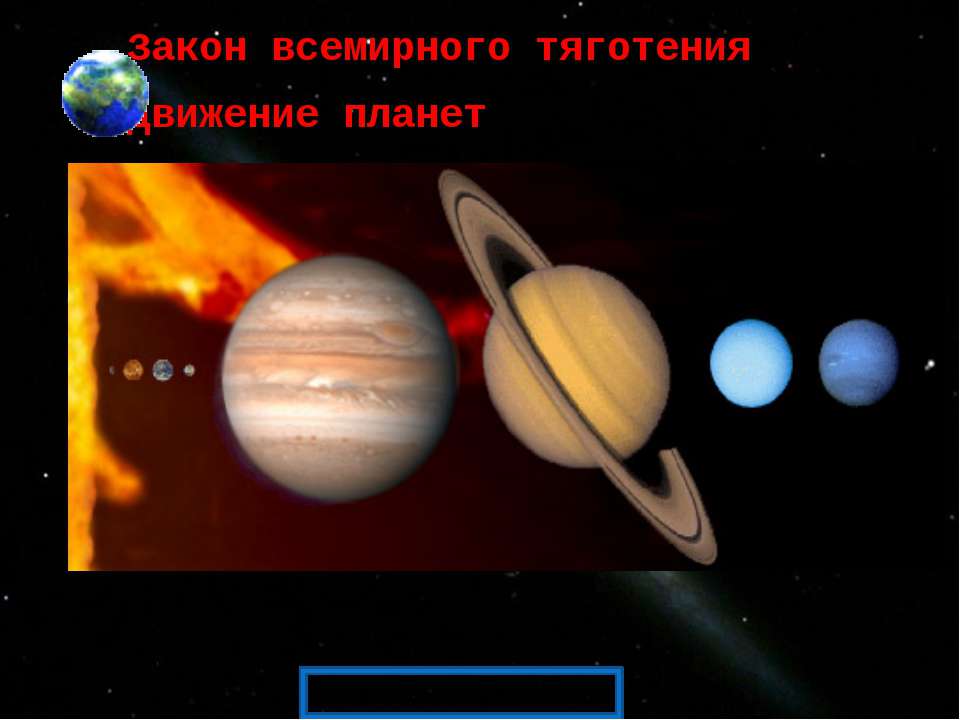
Закон всемирного тяготения. Движение планет
- Рубрика: Презентации / Презентации по Физике
- Просмотров: 260
Презентация для классов "Закон всемирного тяготения. Движение планет" онлайн бесплатно на сайте электронных школьных презентаций uchebniki.org.ua
Закон всемирного тяготения Движение планет Дубов Олег 10 класс Учитель – Касерес М.О Prezentacii.com
Значение Наличие всемирного тяготения: объясняет устойчивость солнечной системы; движение планет и других небесных тел. С открытием закона всемирного тяготения, к людям пришло понимание принципа строения вселенной
События, предшествующие открытию Закона всемирного тяготения Гипотеза Николая Коперника о том, что все планеты движутся вокруг Солнца Сбор эмпирических данных (измерения положения планет, выполненные астрономом Тихо Браге Анализ данных и их обобщение в эмпирических законах, сделанное Иоганном Кеплером Построение теории, объясняющей все общие закономерности и предсказывающей многие новые следствия, сделанное Исааком Ньютоном
Исаак Ньютон (4.1.1643 - 31.3.1727) английский физик и математик Создатель теоретических основ механики и астрономии. Разработал дифференциальное и интегральное исчисления. Изобрел зеркальный телескоп. Автор важнейших экспериментальных работ по оптике. Открыл закон всемирного тяготения.
Формулировка Закона всемирного тяготения Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорционально квадрату расстояния между ними. Английский физик Генри Кавендиш определил, насколько велика сила притяжения между двумя объектами. Для этого он использовал установку, схематически показанную на анимации. В результате была достаточно точно определена гравитационная постоянная, что позволило Кавендишу впервые определить и массу Земли.
Сила F - сила тяжести которая всегда направлена к центру Земли Проявлением закона всемирного тяготения является сила тяжести. На поверхности Земли сила всемирного тяготения, действующая на тело массой m, равна
Границы применимости закона 1) материальных точек; 2) тел, имеющих форму шара; 3) шара большого радиуса, взаимодействующего с телами, размеры которых много меньше размеров шара Сила тяготения очень мала и становится заметной только тогда, когда хотя бы одно из взаимодействующих тел имеет очень большую массу (планета, звезда). Закон всемирного тяготения имеет определенные границы применимости:
Вращение планет вокруг Солнца по законам всемирного тяготения Гравитационное взаимодействие – это взаимодействие ,свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу
Применение Ярчайшим примером применения закона всемирного тяготения является запуск искусственного спутника Земли Спутник все время находится на равном расстоянии над поверхностью Земли Земля притягивает одинаково на всех направлениях
Вращение спутников вокруг Земли по законам всемирного тяготения Двигаясь по круговой орбите радиуса r, на спутник действует сила земного тяготения gmM/r2, где g – постоянная тяготения, m - масса спутника и M - масса планеты. Согласно второму закону Ньютона сила тяготения равна центростремительной силе mv2/r. Двигаясь по круговой орбите радиуса r, на спутник действует сила земного тяготения gmM/r2, где g - постоянная тяготения, m - масса спутника и M - масса планеты (Земли в нашем случае). Согласно второму закону Ньютона сила тяготения равна центростремительной силе mv2/r. Отсюда получаем выражение для скорости движения спутника по круговой орбите: v=(g M/r)1/2 Период обращения спутника вокруг Земли Tсп равен длине орбиты 2pr, делённой на скорость движения спутника v: Tсп=2pr/v=2p (r3/gM)1/2 Если этот орбитальный период Tсп равен периоду вращения Земли вокруг собственной оси (примерно 24 часа), то спутник будет "висеть" над одним и тем же районом Земли, а такая орбита называется геостационарной. Геостационарная орбита лежит в плоскости экватора Земли. Её радиус составляет 42164 км, что примерно в 6 раз больше радиуса Земли. Небесные координаты спутника на геостационарной орбите остаются постоянными и мы можем легко направить на него параболическую антенну (например, для приема спутникового телевидения). Когда радиус орбиты меньше чем радиус геостационарной орбиты, спутник будет обгонять вращение Земли и в этом случае необходимо использовать механизм слежения параболической антенны за положением спутника, что достаточно сложно и дорого для массового применения. Однако, спутники на низких орбитах обеспечивают более мощный сигнал по сравнению с сигналом геостационарных спутников и его можно принимать даже на антенну мобильного телефона. Поэтому возникла идея использовать несколько спутников на одной и той же орбите, которые, заменяя друг друга, будут поддерживать непрерывную связь над каким-то районом Земли. Такой принцип был использован в телекоммуникационной системе "Иридиум", которая состоит из 66 низкоорбитальных спутников: по 11 спутников на 6 орбитах, как показано на анимации. Каждый спутник обеспечивает связь над участком Земли, показанном на анимации светлым пятном. Мы можем видеть, что, перекрываясь, пятна покрывают всю поверхность Земли. Это означает, что такая спутниковая система обеспечивает непрерывную связь из любой точки Земли.
Свободное движение тел в гравитационном поле Земли Максимальная дальность полёта снаряда достигается при стрельбе под углом равном 45°. ДВИЖЕНИЕ ТЕЛ В ПОЛЕ ТЯЖЕСТИ ЗЕМЛИ Рассмотрим движение свободного тела в присутствии гравитационного поля Земли на примере выстрела из пушки. Если пушка расположена в точке с координатами (0, 0, 0), то снаряд будет двигаться по траектории, которая описывается следующими уравнениями: X = (vcosj)t Y = (vsinj)t - gt2/2, где v - скорость снаряда вдоль ствола пушки, j - угол между стволом пушки и горизонтом (ось X), t - время, g - ускорение свободного падения в поле тяжести Земли. Подставляя t из первого уравнения во второе, находим уравнение траектории движения снаряда: Y = X tgj - (g/2v2)(1 + tg2j) X2 Из приведённого выше уравнения видно можно видеть, что траектория полёта снаряда имеет параболическую форму. Из этого уравнения находим максимальную дальность стрельбы Xmax (при этом Y=0) и максимальную высоту полёта Ymax (первая производная Y по координате X равна нулю): Xmax = v2sin(2j)/g Ymax = v2sin2j/2g Из первого уравнения видно, что максимальная дальность полёта снаряда достигается при стрельбе под углом j, равном 45°. На видео-анимации показаны траектории полёта снаряда при стрельбе под углами 30, 45 и 70 градусов.

















