Презентация по математике на тему "Объём пирамиды" 11 класс

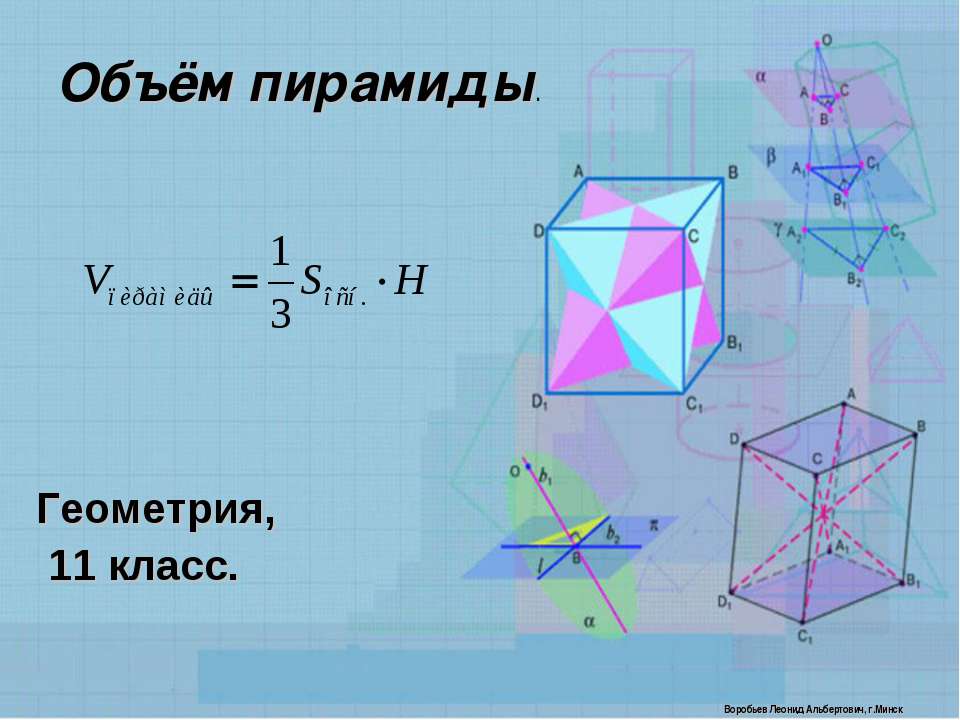
Объем пирамиды.
Тема урока:

г. Воронеж 2022 год
Преподаватель математики: Ширикова Галина Николаевна

Что мы знаем о пирамиде?

Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания – вершины пирамиды и треугольников -боковых граней.

Термин “пирамида” заимствован
из греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как полагают, из египетского языка. В папирусе Ахмеса встречается слово “пирамус” в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от форм хлебцев в Древней Греции “пирос” - рожь). В связи с тем, что форма пламени иногда напоминает образ пирамиды, некоторые средневековые ученые считали, что термин происходит от греческого слова “пир” - огонь. Вот почему в некоторых учебниках геометрии XVI в. пирамида названа “огнеформное тело”.

α
А1
А2
Аn
P
H
Основание
Боковые грани
Вершина
Высота
Боковые ребра

Пирамиды
Треугольная пирамида (тетраэдр)
Шестиугольная пирамида
Четырехугольная пирамида

Пирамида называется правильной, если ее основание - правильный многоугольник , а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Аn
А1
А2
P
h
O
А3

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины
Апофемы
Все апофемы правильной пирамиды равны друг другу

Диагональное сечение пирамиды – сечение плоскостью, проходящей через два не соседних боковых ребра

Площадь пирамиды
Sполн. = Sбок. + Sосн.
Sбок.
Sосн.

h
H

Свойства пирамиды:
У правильной пирамиды:
боковые ребра равны;
боковые грани являются равными равнобедренными треугольниками;
апофемы равны;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему.

Свойства пирамиды:
если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания.
если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.

Теорема: Объём пирамиды равен одной трети произведения площади основания на высоту.
∙

А
D
С
В
О
h
F
Доказательство:

Теорема: Объём усечённой пирамиды, высота которой h, а площади оснований равны S и S₁ вычисляется по формуле.

3
х
1
0
х
В 13
5
0
,
2
Задачи по готовым чертежам

Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .
3
х
1
0
х
В 13
3

Сторона основания правильной треугольной пирамиды равна 6, а боковое ребро образует с плоскостью основания угол 450. Найдите объем пирамиды.
ДОМАШНЕЕ ЗАДАНИЕ
Высота правильной треугольной пирамиды равна , а боковая грань образует с плоскостью основания угол 600. Найдите объем пирамиды.